6 循环神经网络与死亡率预测

😷 新冠肺炎死亡率数据：https://mpidr.shinyapps.io/stmortality/

6.1 Lee-Carter Model

Lee Carter模型中，死亡力（force of mortality）的定义如下：
\[\log \left(m_{t, x}\right)=a_{x}+b_{x} k_{t}\] 其中，

• \(m_{t, x}>0\) 是 \(x\) 岁的人在日历年 \(t\) 的死亡率（mortality rate）,

• \(a_{x}\) 是 \(x\) 岁的人的平均对数死亡率,

• \(b_{x}\) 是死亡率变化的年龄因素,

• \(\left(k_{t}\right)_{t}\) 是死亡率变化的日历年因素.

用 \(M_{t, x}\) 表示某一性别死亡率的观察值（raw mortality rates）.
我们对对数死亡率 \(\log \left(M_{t, x}\right)\) 中心化处理：
\[\log \left(M_{t, x}^{\circ}\right)=\log \left(M_{t, x}\right)-\widehat{a}_{x}=\log \left(M_{t, x}\right)-\frac{1}{|\mathcal{T}|} \sum_{s \in \mathcal{T}} \log \left(M_{s, x}\right)\]

其中，

• \(\mathcal{T}\) 为训练集中日历年的集合,

• \(\widehat{a}_{x}=\frac{1}{|\mathcal{T}|} \sum_{s \in \mathcal{T}} \log \left(M_{s, x}\right)\) 是平均对数死亡率 \(a_{x}\) 的估计.

对于\(b_x,k_t\) 我们的目标是求如下最优化问题：
\[\underset{\left(b_{x}\right)_{x},\left(k_{t}\right)_{t}}{\arg \min } \sum_{t, x}\left(\log \left(M_{t, x}^{\circ}\right)-b_{x} k_{t}\right)^{2}。\]

定义矩阵 \(A=\left(\log \left(M_{t, x}^{\circ}\right)\right)_{x, t}\)。上述最优化问题可以通过对\(A\)进行奇异值分解（SVD）解决\[A=U\Lambda V^\intercal,\] 其中\(U\)称为左奇异矩阵，对角矩阵\(\Lambda=\text{diag}(\lambda_1,\ldots,\lambda_T)\)中的对角元素\(\lambda_1\geq\lambda_2\geq\ldots\geq\lambda_T\geq0\)称为奇异值，\(V\)称为右奇异矩阵。

• \(A\) 的第一个左奇异向量\(U_{\cdot,1}\)与第一个奇异值\(\lambda_1\)相乘，可以得到 \(\left(b_{x}\right)_{x}\) 的一个估计 \(\left(\widehat{b}_{x}\right)_{x}\)。

• \(A\) 的第一个右奇异向量\(V_{\cdot,1}\)给出了 \(\left(k_{t}\right)_{t}\) 的一个估计 \(\left(\widehat{k}_{t}\right)_{t}\)。

为了求解结果的唯一性，增加约束：
\[\sum_{x} \hat{b}_{x}=1 \quad \text { and } \quad \sum_{t \in \mathcal{T}} \hat{k}_{t}=0\] 至此即可解出唯一的 \(\left(\hat{a}_{x}, \hat{b}_{x}\right)_{x}, \left(\hat{k}_{t}\right)_{t}\) . 这就是经典的LC模型构建方法.

6.2 普通循环神经网络（recurrent neural network）

输入变量（Input） : \(\left(\boldsymbol{x}_{1}, \ldots, \boldsymbol{x}_{T}\right)\) with components \(\boldsymbol{x}_{t} \in \mathbb{R}^{\tau_{0}}\) at times \(t=1, \ldots, T\) (in time series structure).

输出变量（Output）: \(y \in \mathcal{Y} \subset \mathbb{R}\) .

首先看一个具有 \(\tau_{1} \in \mathbb{N}\) 个隐层神经元（hidden neurons）和单一隐层（hidden layer）的RNN. 隐层由如下映射（mapping）定义： \[\boldsymbol{z}^{(1)}: \mathbb{R}^{\tau_{0} \times \tau_{1}} \rightarrow \mathbb{R}^{\tau_{1}}, \quad\left(\boldsymbol{x}_{t}, \boldsymbol{z}_{t-1}\right) \mapsto \boldsymbol{z}_{t}^{(1)}=\boldsymbol{z}^{(1)}\left(\boldsymbol{x}_{t}, \boldsymbol{z}_{t-1}\right)\] 其中下标 \(t\) 表示时间,上标 (1) 表示第一隐层（本例中也是唯一隐层）.

隐层结构构造如下：
\[ \begin{aligned} \boldsymbol{z}^{(1)}\left(\boldsymbol{x}_{t}, \boldsymbol{z}_{t-1}\right) =&\left(\phi\left(\left\langle\boldsymbol{w}_{1}^{(1)}, \boldsymbol{x}_{t}\right\rangle+\left\langle\boldsymbol{u}_{1}^{(1)}, \boldsymbol{z}_{t-1}\right\rangle\right), \ldots, \phi\left(\left\langle\boldsymbol{w}_{\tau_{1}}^{(1)}, \boldsymbol{x}_{t}\right\rangle+\left\langle\boldsymbol{u}_{\tau_{1}}^{(1)}, \boldsymbol{z}_{t-1}\right\rangle\right)\right)^{\top} \\ \stackrel{\text { def. }}{=} &\phi\left(\left\langle W^{(1)}, \boldsymbol{x}_{t}\right\rangle+\left\langle U^{(1)}, \boldsymbol{z}_{t-1}\right\rangle\right) \end{aligned} \] 其中第 \(1 \leq j \leq \tau_{1}\) 个神经元的结构为：
\[\phi\left(\left\langle\boldsymbol{w}_{j}^{(1)}, \boldsymbol{x}_{t}\right\rangle+\left\langle\boldsymbol{u}_{j}^{(1)}, \boldsymbol{z}_{t-1}\right\rangle\right)=\phi\left(w_{j, 0}^{(1)}+\sum_{l=1}^{\tau_{0}} w_{j, l}^{(1)} x_{t, l}+\sum_{l=1}^{\tau_{1}} u_{j, l}^{(1)} z_{t-1, l}\right)\]

• \(\phi: \mathbb{R} \rightarrow \mathbb{R}\) 是非线性激活函数（activation function）
• 网络参数（network parameters）为 \[W^{(1)}=\left(\boldsymbol{w}_{j}^{(1)}\right)_{1 \leq j \leq \tau_{1}}^{\top} \in \mathbb{R}^{\tau \times\left(\tau_{0}+1\right)} \text{(including an intercept)}\] \[U^{(1)}=\left(\boldsymbol{u}_{j}^{(1)}\right)_{1 \leq j \leq \tau_{1}}^{\top} \in \mathbb{R}^{\tau_{1} \times \tau_{1}} \text{(excluding an intercept)}\]

除了上述单隐层的结构，我们还可以轻松地设计多隐层的RNN.

例如，双隐层的RNN结构可以为:

• 1st variant : 仅允许同级隐层之间的循环 \[ \begin{aligned} \boldsymbol{z}_{t}^{(1)} &=\boldsymbol{z}^{(1)}\left(\boldsymbol{x}_{t}, \boldsymbol{z}_{t-1}^{(1)}\right) \\ \boldsymbol{z}_{t}^{(2)} &=\boldsymbol{z}^{(2)}\left(\boldsymbol{z}_{t}^{(1)}, \boldsymbol{z}_{t-1}^{(2)}\right) \end{aligned} \]

• 2nd variant : 允许跨级隐层循环 \[ \begin{aligned} \boldsymbol{z}_{t}^{(1)} &=\boldsymbol{z}^{(1)}\left(\boldsymbol{x}_{t}, \boldsymbol{z}_{t-1}^{(1)}, \boldsymbol{z}_{t-1}^{(2)}\right) \\ \boldsymbol{z}_{t}^{(2)} &=\boldsymbol{z}^{(2)}\left(\boldsymbol{z}_{t}^{(1)}, \boldsymbol{z}_{t-1}^{(2)}\right) \end{aligned} \]

• 3rd variant : 允许二级隐层与输入层 \(\boldsymbol{x}_{t}\) 进行循环 \[ \begin{aligned} \boldsymbol{z}_{t}^{(1)} &=\boldsymbol{z}^{(1)}\left(\boldsymbol{x}_{t}, \boldsymbol{z}_{t-1}^{(1)}, \boldsymbol{z}_{t-1}^{(2)}\right) \\ \boldsymbol{z}_{t}^{(2)} &=\boldsymbol{z}^{(2)}\left(\boldsymbol{x}_{t}, \boldsymbol{z}_{t}^{(1)}, \boldsymbol{z}_{t-1}^{(2)}\right) \end{aligned} \]

6.3 长短期记忆神经网络（Long short-term memory）

以上plain vanilla RNN 无法处理长距离依赖和且有梯度消散的问题。为此，Hochreiter-Schmidhuber (1997)提出了长短期记忆神经网络(Long Short Term Memory Network, LSTM)。

6.3.1 激活函数（Activation functions）

LSTM 用到3种不同的 激活函数（activation functions）:

1. Sigmoid函数（Sigmoid function）
   \[\phi_{\sigma}(x)=\frac{1}{1+e^{-x}} \in(0,1)\]

2. 双曲正切函数（Hyberbolic tangent function） \[\phi_{\tanh }(x)=\frac{e^{x}-e^{-x}}{e^{x}+e^{-x}}=2 \phi_{\sigma}(2 x)-1 \in(-1,1)\]

3. 一般的激活函数（General activation function） \[\phi: \mathbb{R} \rightarrow \mathbb{R}\]

6.3.2 Gates and cell state

令 \(\boldsymbol{z}_{t-1}^{(1)} \in \mathbb{R}^{\tau_{1}}\) 表示时间 \((t-1)\) 时的活化状态（neuron activations）. 我们定义3中不同的 门（gates）, 用来决定传播到下一个时间的信息量：

• 遗忘门（Forget gate） (loss of memory rate): \[\boldsymbol{f}_{t}^{(1)}=\boldsymbol{f}^{(1)}\left(\boldsymbol{x}_{t}, \boldsymbol{z}_{t-1}^{(1)}\right)=\phi_{\sigma}\left(\left\langle W_{f}, \boldsymbol{x}_{t}\right\rangle+\left\langle U_{f}, \boldsymbol{z}_{t-1}^{(1)}\right\rangle\right) \in(0,1)^{\tau_{1}}\] for network parameters \(W_{f}^{\top} \in \mathbb{R}^{\tau_{1} \times\left(\tau_{0}+1\right)}\) (including an intercept) \(, U_{f}^{\top} \in \mathbb{R}^{\tau_{1} \times \tau_{1}}\) (excluding an intercept \(),\) and where the activation function is evaluated element wise.

• 输入门（Input gate） (memory update rate): \[\boldsymbol{i}_{t}^{(1)}=\boldsymbol{i}^{(1)}\left(\boldsymbol{x}_{t}, \boldsymbol{z}_{t-1}^{(1)}\right)=\phi_{\sigma}\left(\left\langle W_{i}, \boldsymbol{x}_{t}\right\rangle+\left\langle U_{i}, \boldsymbol{z}_{t-1}^{(1)}\right\rangle\right) \in(0,1)^{\tau_{1}}\] for network parameters \(W_{i}^{\top} \in \mathbb{R}^{\tau_{1} \times\left(\tau_{0}+1\right)}\) (including an intercept), \(U_{i}^{\top} \in \mathbb{R}^{\tau_{1} \times \tau_{1}}\).

• 输出门（Output gate） (release of memory information rate): \[\boldsymbol{o}_{t}^{(1)}=\boldsymbol{o}^{(1)}\left(\boldsymbol{x}_{t}, \boldsymbol{z}_{t-1}^{(1)}\right)=\phi_{\sigma}\left(\left\langle W_{o}, \boldsymbol{x}_{t}\right\rangle+\left\langle U_{o}, \boldsymbol{z}_{t-1}^{(1)}\right\rangle\right) \in(0,1)^{\tau_{1}}\] for network parameters \(W_{o}^{\top} \in \mathbb{R}^{\tau_{1} \times\left(\tau_{0}+1\right)}\) (including an intercept) \(, U_{o}^{\top} \in \mathbb{R}^{\tau_{1} \times \tau_{1}}\).

注意：以上三种门的名字并不代表着它们在实际中的作用，它们的作用由网络参数决定，而网络参数是从数据中学到的。

令 \(\left(\boldsymbol{c}_{t}^{(1)}\right)_{t}\) 表示 细胞状态（cell state） , 用以储存已获得的相关信息.

细胞状态的更新规则如下：
\[\begin{aligned} \boldsymbol{c}_{t}^{(1)}&=\boldsymbol{c}^{(1)}\left(\boldsymbol{x}_{t}, \boldsymbol{z}_{t-1}^{(1)}, \boldsymbol{c}_{t-1}^{(1)}\right)\\&=\boldsymbol{f}_{t}^{(1)} \circ \boldsymbol{c}_{t-1}^{(1)}+\boldsymbol{i}_{t}^{(1)} \circ \phi_{\tanh }\left(\left\langle W_{c}, \boldsymbol{x}_{t}\right\rangle+\left\langle U_{c}, \boldsymbol{z}_{t-1}^{(1)}\right\rangle\right) \in \mathbb{R}^{\tau_{1}} \end{aligned}\] for network parameters \(W_{c}^{\top} \in \mathbb{R}^{\tau_{1} \times\left(\tau_{0}+1\right)}\) (including an intercept), \(U_{c}^{\top} \in \mathbb{R}^{\tau_{1} \times \tau_{1}},\) and \(\circ\) denotes the Hadamard product (element wise product).

最后，我们更新时刻 \(t\) 时的活化状态 \(\boldsymbol{z}_{t}^{(1)} \in \mathbb{R}^{\tau_{1}}\).
\[\boldsymbol{z}_{t}^{(1)}=\boldsymbol{z}^{(1)}\left(\boldsymbol{x}_{t}, \boldsymbol{z}_{t-1}^{(1)}, \boldsymbol{c}_{t-1}^{(1)}\right)=\boldsymbol{o}_{t}^{(1)} \circ \phi\left(\boldsymbol{c}_{t}^{(1)}\right) \in \mathbb{R}^{\tau_{1}}\]

至此，

• 涉及的全部网络参数有: \[W_{f}^{\top}, W_{i}^{\top}, W_{o}^{\top}, W_{c}^{\top} \in \mathbb{R}^{\tau_{1} \times\left(\tau_{0}+1\right)}，~~ U_{f}^{\top}, U_{i}^{\top}, U_{o}^{\top}, U_{c}^{\top} \in \mathbb{R}^{\tau_{1} \times \tau_{1}} .\]

• 一个LSTM层需要 \(4\left(\left(\tau_{0}+1\right) \tau_{1}+\tau_{1}^{2}\right)\) 个网络参数。

• 以上定义的复杂映射在keras通过函数layer_lstm()即可实现。

• 这些参数均由梯度下降的变式算法（a variant of the gradient descent algorithm）学习得.

6.3.3 Output Function

基于 \(\left(\boldsymbol{x}_{1}, \ldots, \boldsymbol{x}_{T}\right)\) , 我们来预测定义在 \(\mathcal{Y} \subset \mathbb{R}\) 的随机变量 \(Y_{T}\) .

\[\widehat{Y}_{T}=\widehat{Y}_{T}\left(\boldsymbol{x}_{1}, \ldots, \boldsymbol{x}_{T}\right)=\varphi\left\langle\boldsymbol{w}, \boldsymbol{z}_{T}^{(1)}\right\rangle \in \mathcal{Y}\] 其中，

• \(z_{T}^{(1)}\) 是最新的隐层神经元活化状态（hidden neuron activation）

• \(\boldsymbol{w} \in \mathbb{R}^{\tau_{1}+1}\) 是输出权重(again including an intercept component)

• \(\varphi: \mathbb{R} \rightarrow \mathcal{Y}\) 是一个恰当的输出激活函数，选择时需要考虑\(y\)的取值范围。

6.3.4 Time-distributed Layer

以上只考虑了根据最新的状态 \(\boldsymbol{z}_{T}^{(1)}\left(\boldsymbol{x}_{1}, \ldots, \boldsymbol{x}_{T}\right)\) 所确定的单一的输出 \(Y_{T}\).

但是我们可以考虑 所有 隐层神经元状态:
\[\boldsymbol{z}_{1}^{(1)}\left(\boldsymbol{x}_{1}\right), \boldsymbol{z}_{2}^{(1)}\left(\boldsymbol{x}_{1}, \boldsymbol{x}_{2}\right), \boldsymbol{z}_{3}^{(1)}\left(\boldsymbol{x}_{1}, \ldots, \boldsymbol{x}_{3}\right), \ldots, \boldsymbol{z}_{T}^{(1)}\left(\boldsymbol{x}_{1}, \ldots, \boldsymbol{x}_{T}\right)\] 每一个状态 \(\boldsymbol{z}_{t}^{(1)}\left(\boldsymbol{x}_{1}, \ldots, \boldsymbol{x}_{t}\right)\) 都可以作为解释变量，用以估计 \(t\) 时所对应的 \(Y_{t}\) :

\[\widehat{Y}_{t}=\widehat{Y}_{t}\left(\boldsymbol{x}_{1}, \ldots, \boldsymbol{x}_{t}\right)=\varphi\left\langle\boldsymbol{w}, \boldsymbol{z}_{t}^{(1)}\right\rangle=\varphi\left\langle\boldsymbol{w}, \boldsymbol{z}_{t}^{(1)}\left(\boldsymbol{x}_{1}, \ldots, \boldsymbol{x}_{t}\right)\right\rangle\] 其中过滤器（filter） \(\varphi\langle\boldsymbol{w}, \cdot\rangle\) 对所有时间 \(t\) 取相同函数.

小结：LSTM的优势

• 时间序列结构和因果关系都可以得到正确的反应

• 由于参数不依赖时间，LSTM可以很容易地拓展到未来时间段

6.4 门控循环神经网络（Gated Recurrent Unit）

另一个比较热门的RNN结构是：门控循环单元（gated recurrent unit, GRU), 由Cho et al. (2014) 提出，它比LSTM更加简洁，但同样可以缓解plain vanilla RNN中梯度消散的问题。

6.4.1 Gates

GRU只使用2个不同的门（gates）. 令 \(\boldsymbol{z}_{t-1}^{(1)} \in \mathbb{R}^{\tau_{1}}\) 表示 \((t-1)\) 时神经元活化状态.

• Reset gate: 类似于LSTM中的遗忘门 \[\boldsymbol{r}_{t}^{(1)}=\boldsymbol{r}^{(1)}\left(\boldsymbol{x}_{t}, \boldsymbol{z}_{t-1}^{(1)}\right)=\phi_{\sigma}\left(\left\langle W_{r}, \boldsymbol{x}_{t}\right\rangle+\left\langle U_{r}, \boldsymbol{z}_{t-1}^{(1)}\right\rangle\right) \in(0,1)^{\tau_{1}}\] for network parameters \(W_{r}^{\top} \in \mathbb{R}^{\tau_{1} \times\left(\tau_{0}+1\right)}\) (including an intercept), \(U_{r}^{\top} \in \mathbb{R}^{\tau_{1} \times \tau_{1}}\).

• Update gate: 类似于LSTM中的输入门 \[\boldsymbol{u}_{t}^{(1)}=\boldsymbol{u}^{(1)}\left(\boldsymbol{x}_{t}, \boldsymbol{z}_{t-1}^{(1)}\right)=\phi_{\sigma}\left(\left\langle W_{u}, \boldsymbol{x}_{t}\right\rangle+\left\langle U_{u}, \boldsymbol{z}_{t-1}^{(1)}\right\rangle\right) \in(0,1)^{\tau_{1}}\] for network parameters \(W_{u}^{\top} \in \mathbb{R}^{\tau_{1} \times\left(\tau_{0}+1\right)}\) (including an intercept), \(U_{u}^{\top} \in \mathbb{R}^{\tau_{1} \times \tau_{1}}\)

6.4.2 Neuron Activations

以上门变量的作用是，已知 \(t-1\) 时神经元活化状态 \(\boldsymbol{z}_{t-1}^{(1)}\), 计算 \(t\) 时神经元活化状态 \(\boldsymbol{z}_{t}^{(1)} \in \mathbb{R}^{\tau_{1}}\) . 我们选用如下结构： \[\boldsymbol{z}_{t}^{(1)}=\boldsymbol{z}^{(1)}\left(\boldsymbol{x}_{t}, \boldsymbol{z}_{t-1}^{(1)}\right)=\boldsymbol{r}_{t}^{(1)} \circ \boldsymbol{z}_{t-1}^{(1)}+\left(\mathbf{1}-\boldsymbol{r}_{t}^{(1)}\right) \circ \phi\left(\left\langle W, \boldsymbol{x}_{t}\right\rangle+\boldsymbol{u}_{t} \circ\left\langle U, \boldsymbol{z}_{t-1}^{(1)}\right\rangle\right) \in \mathbb{R}^{\tau_{1}}\] for network parameters \(W^{\top} \in \mathbb{R}^{\tau_{1} \times\left(\tau_{0}+1\right)}\) (including an intercept) \(, U^{\top} \in \mathbb{R}^{\tau_{1} \times \tau_{1}},\) and where \(\circ\) denotes the Hadamard product.

GRU网络比LSTM网络的结构更简洁，而且会产生相近的结果。 但是，GRU在稳健性上有较大缺陷，因此现阶段LSTM的使用更为广泛.

6.5 案例分析（Case study）

本案例的数据来源于Human Mortality Database (HMD)中的数据，选择瑞士人口数据(HMD中标记为“CHE”)作为示例。

6.5.1 数据描述

数据包含7个变量，各变量说明如下：

变量	类型	说明
Gender	factor	两种性别——男性和女性
Year	int	日历年，1950年到2016年
Age	int	年龄范围0-99岁
Country	chr	“CHE”，代表瑞士
imputed_flag	logi	原始死亡率为0，用HMD中其余国家同日历年同年龄的平均死亡率代替，则该变量为TRUE
mx	num	死亡率
logmx	num	对数死亡率

path.data <- "6 - Lee and Carter go Machine Learning Recurrent Neural Networks/CHE_mort.csv"           # path and name of data file
region <- "CHE"                    # country to be loaded (code is for one selected country)
source(file="6 - Lee and Carter go Machine Learning Recurrent Neural Networks/00_a package - load data.R")
str(all_mort)
length(unique(all_mort$Age))
length(unique(all_mort$Year))
67*2*100

6.5.2 死亡率热力图

gender <- "Male"
#gender <- "Female"
m0 <- c(min(all_mort$logmx), max(all_mort$logmx))
# rows are calendar year t, columns are ages x
logmx <- t(matrix(as.matrix(all_mort[which(all_mort$Gender==gender),"logmx"]), nrow=100, ncol=67))
# png("./plots/6/heat.png")
image(z=logmx, useRaster=TRUE,  zlim=m0, col=rev(rainbow(n=60, start=0, end=.72)), xaxt='n', yaxt='n', main=list(paste("Swiss ",gender, " raw log-mortality rates", sep=""), cex=1.5), cex.lab=1.5, ylab="age x", xlab="calendar year t")
axis(1, at=c(0:(2016-1950))/(2016-1950), c(1950:2016))                   
axis(2, at=c(0:49)/50, labels=c(0:49)*2)                   
lines(x=rep((1999-1950+0.5)/(2016-1950), 2), y=c(0:1), lwd=2)
dev.off()

图6.1显示了男女性对数死亡率随时间的改善:

• 左右两幅图的色标相同，蓝色表示死亡率小，红色表示死亡率大

• 该图显示过去几十年典型的死亡率改善——热图中颜色呈略微向上的对角线结构

• 平均而言，女性死亡率低于男性

• 图中位于2000年的垂直黑线表示对于训练数据\(\mathcal{T}\)和验证数据\(\mathcal{V}\)的划分:后续模型将使用日历年\(t=1950, \ldots, 1999\)作为训练数据\(\mathcal{T}\)进行学习，用\(2000, \ldots, 2016\)作为验证数据\(\mathcal{V}\)对死亡率做样本外验证。

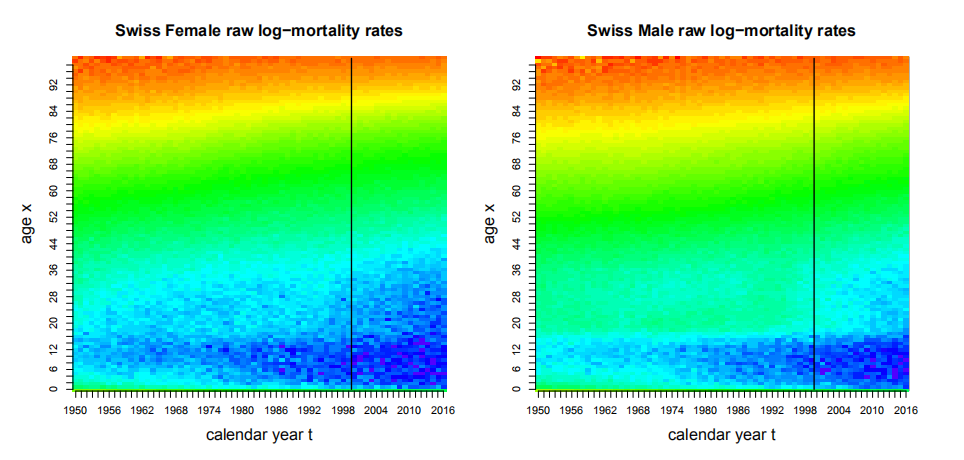
Figure 6.1: 瑞士男女性死亡率热力图

6.5.3 Lee-Carter 模型

ObsYear <- 1999
gender <- "Female"
train <- all_mort[Year<=ObsYear][Gender == gender]
min(train$Year)
    
### fit via SVD
train[,ax:= mean(logmx), by = (Age)]
train[,mx_adj:= logmx-ax]  
rates_mat <- as.matrix(train %>% dcast.data.table(Age~Year, value.var = "mx_adj", sum))[,-1]
dim(rates_mat)
svd_fit <- svd(rates_mat)
    
ax <- train[,unique(ax)]
bx <- svd_fit$u[,1]*svd_fit$d[1]
kt <- svd_fit$v[,1]
      
c1 <- mean(kt)
c2 <- sum(bx)
ax <- ax+c1*bx
bx <- bx/c2
kt <- (kt-c1)*c2
    
### extrapolation and forecast
vali  <- all_mort[Year>ObsYear][Gender == gender]    
t_forecast <- vali[,unique(Year)] %>% length()
forecast_kt  =kt %>% forecast::rwf(t_forecast, drift = T)
kt_forecast = forecast_kt$mean
 
# illustration selected drift
plot_data <- c(kt, kt_forecast)
plot(plot_data, pch=20, col="red", cex=2, cex.lab=1.5, xaxt='n', ylab="values k_t", xlab="calendar year t", main=list(paste("estimated process k_t for ",gender, sep=""), cex=1.5)) 
points(kt, col="blue", pch=20, cex=2)
axis(1, at=c(1:length(plot_data)), labels=c(1:length(plot_data))+1949)                   
abline(v=(length(kt)+0.5), lwd=2)
# in-sample and out-of-sample analysis    
fitted = (ax+(bx)%*%t(kt)) %>% melt
train$pred_LC_svd = fitted$value %>% exp
fitted_vali = (ax+(bx)%*%t(kt_forecast)) %>% melt
vali$pred_LC_svd =   fitted_vali$value %>% exp
round(c((mean((train$mx-train$pred_LC_svd)^2)*10^4) , (mean((vali$mx-vali$pred_LC_svd)^2)*10^4)),4)

用带漂移项的随机游走预测\(t \in \mathcal{V}=\{2000, \ldots, 2016\}\)的\(\hat{k}_{t}\)，下图说明了结果。

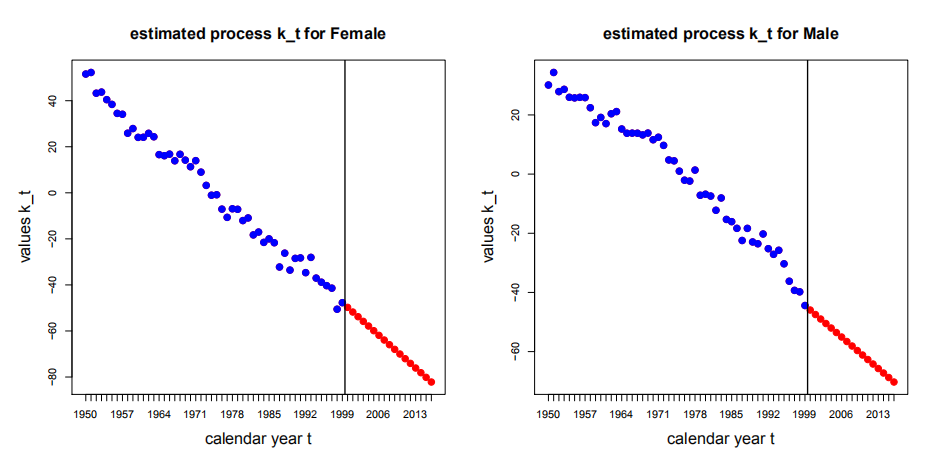
Figure 6.2: 瑞士男女性kt的估计与预测值

图6.2显示对于女性来说预测结果是相对合理的，但是对于男性而言，由此产生的漂移可能需要进一步的探索，下面男女性样本内外的MSE损失结果也表明了这一点：男性样本外损失较大

\[ \begin{array}{|c|cc|cc|} \hline & \ {\text { in-sample loss }} & \ {\text { in-sample loss }} & \ {\text { out-of-sample loss }} & \ {\text { out-of-sample loss }}\\ & \text { female } & \text { male } & \text { female } & \text { male } \\ \hline \text { LC model with SVD } & 3.7573 & 8.8110 & 0.6045 & 1.8152 \\ \hline \end{array} \]

6.5.4 初试RNN

1. 数据说明

• 选择性别为“女性”，提取\(1990, \ldots, 2001\)年的对数死亡率，年龄为\(0 \leq x \leq 99\)

• 超参数设置：回顾周期\(T=10\)；\(\tau_{0}=3\)

• 定义解释变量和响应变量：

  对于\(1 \leq x \leq 98\)，\(1 \leq t \leq T\)，有

  解释变量\(\boldsymbol{x}_{t, x}=\left(\log \left(M_{1999-(T-t), x-1}\right), \log \left(M_{1999-(T-t), x}\right), \log \left(M_{1999-(T-t), x+1}\right)\right)^{\top} \in \mathbb{R}^{\tau_{0}}\)

  响应变量\(\boldsymbol{Y}_{T, x}=\log(M_{2000,x}) =\log \left(M_{1999-(T-T)+1, x}\right) \in \mathbb{R}_{-}\)

  同时考虑\((x-1,x,x+1)\)目的是用邻近的年龄来平滑输入。

• 选择训练数据和验证数据：

  训练数据\(\mathcal{T}=\{(\boldsymbol{x}_{1,x}, \ldots,\boldsymbol{x}_{T,x};\boldsymbol{Y}_{T, x});1 \leq x \leq 98\}\)

  验证数据\(\mathcal{V}=\{(\boldsymbol{x}_{2,x}, \ldots,\boldsymbol{x}_{T+1,x};\boldsymbol{Y}_{T+1, x});1 \leq x \leq 98\}\)，在训练数据基础上时移了一个日历年

• 数据如下图所示：

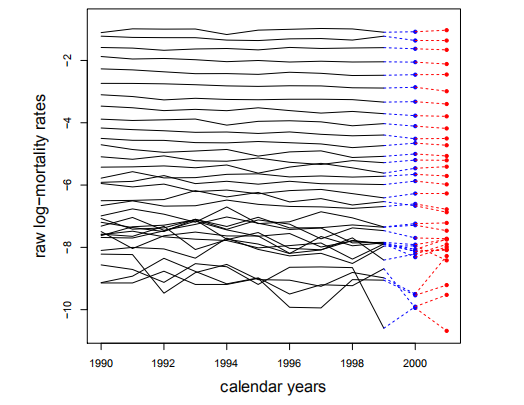
Figure 5.1: RNN初试中选择的数据

黑线表示选定的解释变量\(\boldsymbol{x}_{t, x}\);蓝色的点是训练数据中的的响应变量\(\boldsymbol{Y}_{T, x}\)；验证数据中响应变量\(\boldsymbol{Y}_{T+1, x}=\log(M_{2001,x})\)用红色的点表示

2. 数据预处理

• 对解释变量应用MinMaxScaler进行标准化处理

• 切换响应变量的符号

3. 比较LSTMs和GRUs

• 在验证集\(\mathcal{V}\)上跟踪过拟合

• 梯度下降优化算法选用的是nadam

• 下图显示了5个模型的收敛行为

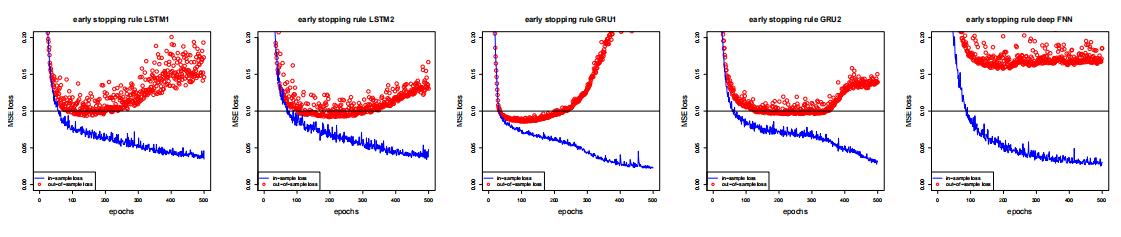
Figure 6.3: 模型的样本内外损失

• 根据过拟合确定的停止时间的模型校准结果如下表所示：

\[ \begin{array}{|l|ccc|cc|} \hline & \# \text { param. } & \text { epochs } & \text { run time } & \text { in-sample loss } & \text { out-of-sample loss } \\ \hline \text { LSTM1 } & 186 & 150 & 8 \mathrm{sec} & 0.0655 & 0.0936 \\ \text { LSTM2 } & 345 & 200 & 15 \mathrm{sec} & 0.0603 & 0.0918 \\ \hline \text { GRU1 } & 141 & 100 & 5 \mathrm{sec} & 0.0671 & 0.0860 \\ \text { GRU2 } & 260 & 200 & 14 \mathrm{sec} & 0.0651 & 0.0958 \\ \hline \text { deep FNN } & 184 & 200 & 5 \mathrm{sec} & 0.0485 & 0.1577 \\ \hline \end{array} \]

• 表中所示模型的超参数设置

1. LSTM1和GRU1表示只有一个隐藏层的RNN，该隐藏层的神经元个数\(\tau_{1}=5\)

2. LSTM2和GRU2表示有两个隐藏层的RNN，第一个隐藏层神经元个数\(\tau_{1}=5\)；第二个隐藏层神经元个数\(\tau_{2}=4\)

3. deep FNN表示有两个隐藏层的前馈神经网络结构，其中\((q1,q2)=(5,4)\)

• 结论

1. LSTM2与LSTM1模型预测质量相当，但LSTM2有更多参数及更长的运行时间

2. LTSM与GRU超参数选择相同时，普遍的观察结果是GRU比LSTM更快的过拟合，但GRU不稳定

3. 前馈神经网络与RNN相比没有竞争力

• 在本文建模中未引入年龄变量的原因：

协变量标准化到（-1,1）的过程是在所有年龄上同时进行的，因此协变量信息保留了死亡率水平，这和引入年龄变量具有相同的信息质量。

4. 超参数选择

• 分别改变\(T、\tau_{0}、\tau_{1}\)的值，得到结果如下表所示：

\[ \begin{array}{|l|ccc|cc|} \hline & \text { # param. } & \text { epochs } & \text { run time } & \text { in-sample } & \text { out-of-sample } \\ \hline \text { base case: } & & & & & \\ \text { LSTM1 }\left(T=10, \tau_{0}=3, \tau_{1}=5\right) & 186 & 150 & 8 \mathrm{sec} & 0.0655 & 0.0936 \\ \hline \text { LSTM1 }\left(T=10, \tau_{0}=1, \tau_{1}=5\right) & 146 & 100 & 5 \mathrm{sec} & 0.0647 & 0.1195 \\ \text { LSTM1 }\left(T=10, \tau_{0}=5, \tau_{1}=5\right) & 226 & 150 & 15 \mathrm{sec} & 0.0583 & 0.0798 \\ \hline \text { LSTM1 }\left(T=5, \tau_{0}=3, \tau_{1}=5\right) & 186 & 100 & 4 \mathrm{sec} & 0.0753 & 0.1028 \\ \text { LSTM1 }\left(T=20, \tau_{0}=3, \tau_{1}=5\right) & 186 & 200 & 16 \mathrm{sec} & 0.0626 & 0.0968 \\ \hline \text { LSTM1 }\left(T=10, \tau_{0}=3, \tau_{1}=3\right) & 88 & 200 & 10 \mathrm{sec} & 0.0694 & 0.0987 \\ \text { LSTM1 }\left(T=10, \tau_{0}=3, \tau_{1}=10\right) & 571 & 100 & 5 \mathrm{sec} & 0.0626 & 0.0883 \\ \hline \end{array} \]

• 结论

1. 分别令\(\tau_{0}=1,3,5\),需要更长的运行时间并提供更好的样本外结果；

2. 分别令\(T=5,10,20\)，结论同上；

3. 分别令\(\tau_{1}=3,5,10\)，导致更快的收敛，因为梯度下降算法有更多的自由度

4. 最大的影响是通过设定一个更大的\(\tau_{0}\)而产生的，因此后面RNN示例中设定\(\tau_{0}=5\)

# load corresponding data
path.data <- "6 - Lee and Carter go Machine Learning Recurrent Neural Networks/CHE_mort.csv"           # path and name of data file
region <- "CHE"                    # country to be loaded (code is for one selected country)
source(file="6 - Lee and Carter go Machine Learning Recurrent Neural Networks/00_a package - load data.R")
str(all_mort)
# LSTMs and GRUs
source(file="6 - Lee and Carter go Machine Learning Recurrent Neural Networks/00_b package - network definitions.R")
T0 <- 10
tau0 <- 3
tau1 <- 5
tau2 <- 4
summary(LSTM1(T0, tau0, tau1, 0, "nadam"))
summary(LSTM2(T0, tau0, tau1, tau2, 0, "nadam"))
summary(LSTM_TD(T0, tau0, tau1, 0, "nadam"))
summary(GRU1(T0, tau0, tau1, 0, "nadam"))
summary(GRU2(T0, tau0, tau1, tau2, 0, "nadam"))
summary(FNN(T0, tau0, tau1, tau2, 0, "nadam"))
# Bringing the data in the right structure for a toy example
gender <- "Female"
ObsYear <- 2000
mort_rates <- all_mort[which(all_mort$Gender==gender), c("Year", "Age", "logmx")] 
mort_rates <- dcast(mort_rates, Year ~ Age, value.var="logmx")
dim(mort_rates)
T0 <- 10     # lookback period
tau0 <- 3    # dimension of x_t (should be odd for our application)
delta0 <- (tau0-1)/2
toy_rates <- as.matrix(mort_rates[which(mort_rates$Year %in% c((ObsYear-T0):(ObsYear+1))),])
dim(toy_rates)
xt <- array(NA, c(2,ncol(toy_rates)-tau0, T0, tau0))
YT <- array(NA, c(2,ncol(toy_rates)-tau0))
for (i in 1:2){for (a0 in 1:(ncol(toy_rates)-tau0)){ 
    xt[i,a0,,] <- toy_rates[c(i:(T0+i-1)),c((a0+1):(a0+tau0))]
    YT[i,a0] <- toy_rates[T0+i,a0+1+delta0]
}}
dim(xt)
dim(YT)
plot(x=toy_rates[1:T0,1], y=toy_rates[1:T0,2], col="white", xlab="calendar years", ylab="raw log-mortality rates", cex.lab=1.5, cex=1.5, main=list("data toy example", cex=1.5), xlim=range(toy_rates[,1]), ylim=range(toy_rates[,-1]), type='l')
for (a0 in 2:ncol(toy_rates)){
  if (a0 %in% (c(1:100)*3)){
    lines(x=toy_rates[1:T0,1], y=toy_rates[1:T0,a0])    
    points(x=toy_rates[(T0+1):(T0+2),1], y=toy_rates[(T0+1):(T0+2),a0], col=c("blue", "red"), pch=20)
    lines(x=toy_rates[(T0):(T0+1),1], y=toy_rates[(T0):(T0+1),a0], col="blue", lty=2)
    lines(x=toy_rates[(T0+1):(T0+2),1], y=toy_rates[(T0+1):(T0+2),a0], col="red", lty=2)
    }}
# LSTMs and GRUs
x.train <- array(2*(xt[1,,,]-min(xt))/(max(xt)-min(xt))-1, c(ncol(toy_rates)-tau0, T0, tau0))
x.vali  <- array(2*(xt[2,,,]-min(xt))/(max(xt)-min(xt))-1, c(ncol(toy_rates)-tau0, T0, tau0))
y.train <- - YT[1,]
(y0 <- mean(y.train))
y.vali  <- - YT[2,]
dim(x.train)
length(y.train);length(y.vali)
# x.age.train<-as.matrix(0:0)
# x.training<-list(x.train,x.age.train)
# x.age.valid<-as.matrix(0:0)
# x.validation<-list(x.vali,x.age.valid)
### examples
tau1 <- 5    # dimension of the outputs z_t^(1) first RNN layer
tau2 <- 4    # dimension of the outputs z_t^(2) second RNN layer
CBs <- callback_model_checkpoint("./6 - Lee and Carter go Machine Learning Recurrent Neural Networks/CallBack/best_model", monitor = "val_loss", verbose = 0,  save_best_only = TRUE, save_weights_only = TRUE,save_freq = NULL)
model <- LSTM2(T0, tau0, tau1, tau2, y0, "nadam")     
summary(model)
# takes 40 seconds on my laptop
{t1 <- proc.time()
  fit <- model %>% fit(x=x.train, y=y.train, validation_data=list(x.vali, y.vali), batch_size=10, epochs=500, verbose=1, callbacks=CBs)
 proc.time()-t1}
plot(fit[[2]]$val_loss,col="red", ylim=c(0,0.5), main=list("early stopping rule", cex=1.5),xlab="epochs", ylab="MSE loss", cex=1.5, cex.lab=1.5)
lines(fit[[2]]$loss,col="blue")
abline(h=0.1, lty=1, col="black")
legend(x="bottomleft", col=c("blue","red"), lty=c(1,-1), lwd=c(1,-1), pch=c(-1,1), legend=c("in-sample loss", "out-of-sample loss"))
load_model_weights_hdf5(model, "./6 - Lee and Carter go Machine Learning Recurrent Neural Networks/CallBack/best_model")
Yhat.train1 <- as.vector(model %>% predict(x.train))
Yhat.vali1 <- as.vector(model %>% predict(x.vali))
c(round(mean((Yhat.train1-y.train)^2),4), round(mean((Yhat.vali1-y.vali)^2),4))

6.5.5 RNN

1. 数据预处理

• 观察值：1950-1999年数据；预测值：2000-2016年对数死亡率

• 分别对男性和女性建立模型，先选定一个性别

• 参数设置：回顾周期\(T=10\)；\(\tau_{0}=5\)

• 定义解释变量（需扩充年龄界限——复制边缘特征值）：

  对于\(0 \leq x \leq 99\)，\(1950 \leq t \leq 1999\)，有

  解释变量\(\boldsymbol{x}_{t, x}=\left(\log \left(M_{t,(x-2) \vee 0}\right), \log \left(M_{t,(x-1) \vee 0}\right), \log \left(M_{t, x}\right), \log \left(M_{t,(x+1) \wedge 99}\right), \log \left(M_{t,(x+2) \wedge 99}\right)\right)^{\top} \in \mathbb{R}^{5}\)

  该式中：\(x_{0}\vee x_{1}=\text {max}\{x_{0},x_{1}\}\);\(x_{0}\wedge x_{1}=\text {min}\{x_{0},x_{1}\}\)

• 定义训练数据\(\mathcal{T}\)和验证数据\(\mathcal{V}\)：

  训练数据\(\mathcal{T}=\{(\boldsymbol{x}_{t-T,x}, \ldots,\boldsymbol{x}_{t-1,x},\boldsymbol{Y}_{t, x});0 \leq x \leq 99\ , 1950+T \leq t \leq 1999\}\)

  其中，\(\boldsymbol{Y}_{t, x}=\text {log}(M_{t,x})\)

  验证数据:

  \(s>1999\)的特征值要用相应的预测值替代

\[ \widehat{\boldsymbol{x}}_{s, x}=\left(\log \left(\widehat{M}_{s,(x-2) \vee 0}\right), \log \left(\widehat{M}_{s,(x-1) \vee 0}\right), \log \left(\widehat{M}_{s, x}\right), \log \left(\widehat{M}_{s,(x+1) \wedge 99}\right), \log \left(\widehat{M}_{s,(x+2) \wedge 99}\right)\right)^{\top} \in \mathbb{R}^{5} \]

因此验证数据\(\mathcal{V}=\{(\boldsymbol{x}_{t-T,x}, \ldots,\boldsymbol{x}_{1999,x},\widehat{\boldsymbol{x}}_{2000,x}, \ldots,\widehat{\boldsymbol{x}}_{t-1,x},\boldsymbol{Y}_{t, x});0 \leq x \leq 99\ , 2000 \leq t \leq 2016\}\)

• 基于训练数据所有特征值的最大最小值对训练数据和验证数据应用MinMaxScaler

• 切换响应变量符号

2. 建立单个性别的RNN

• 将训练数据\(\mathcal T\)随机划分学习集\(\mathcal T_{0}\)(包含80%数据)以及测试集\(\mathcal T_{1}\)(包含20%数据)\(\mathcal T_{0}\)用于追踪样本内过拟合；

• 建立具有三个隐藏层的LSTM3和GRU3；

• 超参数设置：\(T=10\)；\(\tau_{0}=5\)；\(\tau_{1}=20\)；\(\tau_{2}=15\)；\(\tau_{3}=10\)；

• 下图显示了分别对男性和女性建立两个模型的收敛行为

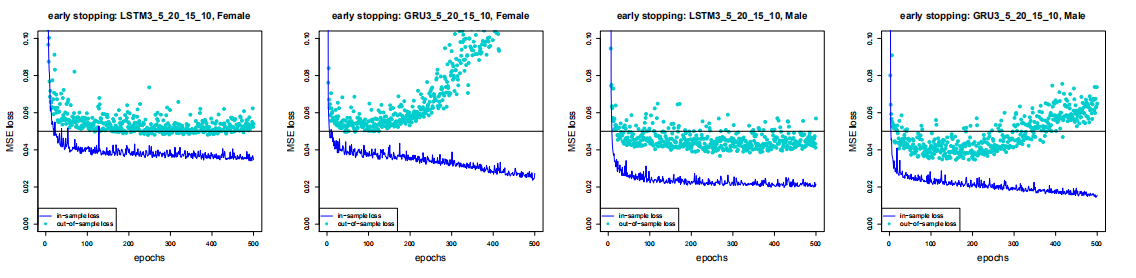
Figure 6.4: 模型的样本内外损失

该图显示：GRU结构会导致更快的收敛，但后续会证实GRU结构不稳定，因此LSTM会更受欢迎

• 下表给出三个模型(LSTM3/GRU3/LC)分性别的样本内外损失

\[ \begin{array}{|l|cc|cc|cc|} \hline & {\text { in-sample }} & {\text { in-sample }} & {\text { out-of-sample }} & {\text { out-of-sample }}& {\text { run times }}& {\text { run times }} \\ & \text { female } & \text { male } & \text { female } & \text { male } & \text { female } & \text { male } \\ \hline \hline \text { LSTM3 }\left(T=10,\left(\tau_{0}, \tau_{1}, \tau_{2}, \tau_{3}\right)=(5,20,15,10)\right) & 2.5222 & 6.9458 & 0.3566 & 1.3507 & 225 \mathrm{s} & 203 \mathrm{s} \\ \text { GRU3 }\left(T=10,\left(\tau_{0}, \tau_{1}, \tau_{2}, \tau_{3}\right)=(5,20,15,10)\right) & 2.8370 & 7.0907 & 0.4788 & 1.2435 & 185 \mathrm{s} & 198 \mathrm{s} \\ \hline \hline \text { LC model with SVD } & 3.7573 & 8.8110 & 0.6045 & 1.8152 & - & - \\ \hline \end{array} \]

能够看到，所有被选择RNN模型都优于LC模型的预测

3. 探索RNN的预测中隐含的漂移项

1. 中心化RNN预测的对数死亡率

\[ \log \left(\widehat{M}_{t, x}^{\circ}\right)=\log(\widehat M_{t,x})-\widehat a_{x} \]

2. 利用下式求得\(2000 \leq t \leq 2016\)对应的\(k_{t}\)

\[ \underset{k_{t}}{\arg \min } \sum_{x}\left(\log \left(\widehat{M}_{t, x}^{\circ}\right)-\widehat{b}_{x} k_{t}\right)^{2} \]

式中，\((\widehat{b}_{x})_{x}\)是从LC模型估计得到的。

3. 估计结果如下图所示

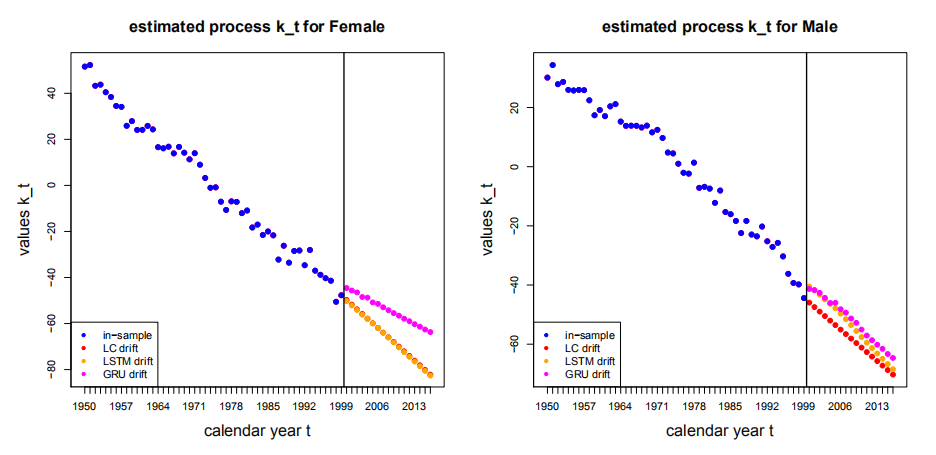
Figure 6.5: 三种模型下kt的估计与预测值

该图显示：对于女性，LSTM3的预测与LC的预测基本一致；而对于男性，LSTM3的预测的斜率略大于LC的预测并收敛与LC的预测；但是GRU3的结果并不令人信服，可能是因为从LC模型中得到的不随时间变化的参数bx的估计与GRU3模型产生的预测不符。

# load corresponding data
path.data <- "6 - Lee and Carter go Machine Learning Recurrent Neural Networks/CHE_mort.csv"           # path and name of data file
region <- "CHE"                    # country to be loaded (code is for one selected country)
source(file="6 - Lee and Carter go Machine Learning Recurrent Neural Networks/00_a package - load data.R")
str(all_mort)
source(file="6 - Lee and Carter go Machine Learning Recurrent Neural Networks/00_b package - network definitions.R")
source(file="6 - Lee and Carter go Machine Learning Recurrent Neural Networks/00_c package - data preparation RNNs.R")
# choice of parameters
T0 <- 10
tau0 <- 5
gender <- "Female"
ObsYear <- 1999
# training data pre-processing 
data1 <- data.preprocessing.RNNs(all_mort, gender, T0, tau0, ObsYear)
dim(data1[[1]])
dim(data1[[2]])
# validation data pre-processing
all_mort2 <- all_mort[which((all_mort$Year > (ObsYear-10))&(Gender==gender)),]
all_mortV <- all_mort2
vali.Y <- all_mortV[which(all_mortV$Year > ObsYear),]
 
# MinMaxScaler data pre-processing
x.min <- min(data1[[1]])
x.max <- max(data1[[1]])
x.train <- array(2*(data1[[1]]-x.min)/(x.min-x.max)-1, dim(data1[[1]]))
y.train <- - data1[[2]]
y0 <- mean(y.train)
# LSTM architectures
# network architecture deep 3 network
tau1 <- 20
tau2 <- 15
tau3 <- 10
optimizer <- 'adam'
# choose either LSTM or GRU network
RNN.type <- "LSTM"
#RNN.type <- "GRU"
{if (RNN.type=="LSTM"){model <- LSTM3(T0, tau0, tau1, tau2, tau3, y0, optimizer)}else{model <- GRU3(T0, tau0, tau1, tau2, tau3, y0, optimizer)}
 name.model <- paste(RNN.type,"3_", tau0, "_", tau1, "_", tau2, "_", tau3, sep="")
 file.name <- paste("./6 - Lee and Carter go Machine Learning Recurrent Neural Networks/CallBack/best_model_", name.model,"_", gender, sep="")
 summary(model)}
# define callback
CBs <- callback_model_checkpoint(file.name, monitor = "val_loss", verbose = 0,  save_best_only = TRUE, save_weights_only = TRUE, save_freq = NULL)
# gradient descent fitting: takes roughly 200 seconds on my laptop
{t1 <- proc.time()
  fit <- model %>% fit(x=x.train, y=y.train, validation_split=0.2,
                                        batch_size=100, epochs=500, verbose=1, callbacks=CBs)                                        
proc.time()-t1}
# plot loss figures
plot.losses(name.model, gender, fit[[2]]$val_loss, fit[[2]]$loss)
# calculating in-sample loss: LC is c(Female=3.7573, Male=8.8110)
load_model_weights_hdf5(model, file.name)
round(10^4*mean((exp(-as.vector(model %>% predict(x.train)))-exp(-y.train))^2),4)
# calculating out-of-sample loss: LC is c(Female=0.6045, Male=1.8152)
pred.result <- recursive.prediction(ObsYear, all_mort2, gender, T0, tau0, x.min, x.max, model)
vali <- pred.result[[1]][which(all_mort2$Year > ObsYear),]
round(10^4*mean((vali$mx-vali.Y$mx)^2),4)

6.5.6 引入性别协变量

1. 数据预处理

• 添加性别指示变量：0表示女性；1表示男性

• 在训练数据时交替使用性别

• 应用MinMaxScaler时的最大最小值是同时考虑两种性别所有训练数据的情况下得到的。

• 模型结构及超参数设置与单个性别RNN相同

2. 建立模型

• 基于使得测试损失最小的LSTM3和GRU模型，预测1999年之后的死亡率，并在特征变量中加入性别指标，下表列出了相应的损失

\[ \begin{array}{|l|c|cc|c|} \hline & {\text { in-sample }} & {\text { out-of-sample }} & {\text { out-of-sample }}& {\text { run times }}\\ & \text {both genders} & \text { female } & \text { male } & \text {both genders} \\ \hline \hline \text { LSTM3 }\left(T=10,\left(\tau_{0}, \tau_{1}, \tau_{2}, \tau_{3}\right)=(5,20,15,10)\right) & 4.7643 & 0.3402 & 1.1346 & 404 \mathrm{s}\\ \text { GRU3 }\left(T=10,\left(\tau_{0}, \tau_{1}, \tau_{2}, \tau_{3}\right)=(5,20,15,10)\right) & 4.6311 & 0.4646 & 1.2571 & 379 \mathrm{s} \\ \hline \hline \text { LC model with SVD } & 6.2841 & 0.6045 &1.8152 & - \\ \hline \end{array} \]

与LC模型相比，得到了一个有很大改进的模型，至少对未来16年的预测是这样的；此外，引入性别协变量的LSTM模型也优于单个性别的模型。

3. 隐含的漂移项

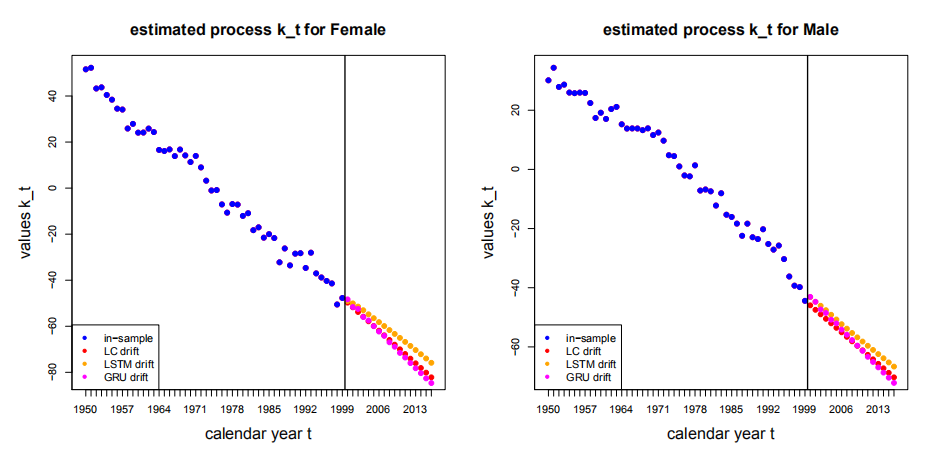
Figure 6.6: 引入性别协变量建模的kt的估计与预测值

# load corresponding data
path.data <- "6 - Lee and Carter go Machine Learning Recurrent Neural Networks/CHE_mort.csv"           # path and name of data file
region <- "CHE"                    # country to be loaded (code is for one selected country)
source(file="6 - Lee and Carter go Machine Learning Recurrent Neural Networks/00_a package - load data.R")
str(all_mort)
source(file="6 - Lee and Carter go Machine Learning Recurrent Neural Networks/00_b package - network definitions.R")
source(file="6 - Lee and Carter go Machine Learning Recurrent Neural Networks/00_c package - data preparation RNNs.R")
# choice of parameters
T0 <- 10
tau0 <- 5
ObsYear <- 1999
# training data pre-processing 
data1 <- data.preprocessing.RNNs(all_mort, "Female", T0, tau0, ObsYear)
data2 <- data.preprocessing.RNNs(all_mort, "Male", T0, tau0, ObsYear)
xx <- dim(data1[[1]])[1]
x.train <- array(NA, dim=c(2*xx, dim(data1[[1]])[c(2,3)]))
y.train <- array(NA, dim=c(2*xx))
gender.indicator <- rep(c(0,1), xx)
for (l in 1:xx){
   x.train[(l-1)*2+1,,] <- data1[[1]][l,,]
   x.train[(l-1)*2+2,,] <- data2[[1]][l,,]
   y.train[(l-1)*2+1] <- -data1[[2]][l]
   y.train[(l-1)*2+2] <- -data2[[2]][l]
          }
# MinMaxScaler data pre-processing
x.min <- min(x.train)
x.max <- max(x.train)
x.train <- list(array(2*(x.train-x.min)/(x.min-x.max)-1, dim(x.train)), gender.indicator)
y0 <- mean(y.train)
# validation data pre-processing
all_mort2.Female <- all_mort[which((all_mort$Year > (ObsYear-10))&(Gender=="Female")),]
all_mortV.Female <- all_mort2.Female
vali.Y.Female <- all_mortV.Female[which(all_mortV.Female$Year > ObsYear),]
all_mort2.Male <- all_mort[which((all_mort$Year > (ObsYear-10))&(Gender=="Male")),]
all_mortV.Male <- all_mort2.Male
vali.Y.Male <- all_mortV.Male[which(all_mortV.Male$Year > ObsYear),]
# LSTM architectures
# network architecture deep 3 network
tau1 <- 20
tau2 <- 15
tau3 <- 10
optimizer <- 'adam'
# choose either LSTM or GRU network
RNN.type <- "LSTM"
#RNN.type <- "GRU"
{if (RNN.type=="LSTM"){model <- LSTM3.Gender(T0, tau0, tau1, tau2, tau3, y0, optimizer)}else{model <- GRU3.Gender(T0, tau0, tau1, tau2, tau3, y0, optimizer)}
 name.model <- paste(RNN.type,"3_", tau0, "_", tau1, "_", tau2, "_", tau3, sep="")
 #file.name <- paste("./Model_Full_Param/best_model_", name.model, sep="")
 file.name <- paste("./6 - Lee and Carter go Machine Learning Recurrent Neural Networks/CallBack/best_model_", name.model, sep="")
 summary(model)}
# define callback
CBs <- callback_model_checkpoint(file.name, monitor = "val_loss", verbose = 0,  save_best_only = TRUE, save_weights_only = TRUE,save_freq = NULL)
# gradient descent fitting: takes roughly 400 seconds on my laptop
{t1 <- proc.time()
  fit <- model %>% fit(x=x.train, y=y.train, validation_split=0.2,
                                        batch_size=100, epochs=500, verbose=1, callbacks=CBs)                                        
proc.time()-t1}
# plot loss figures
plot.losses(name.model, "Both", fit[[2]]$val_loss, fit[[2]]$loss)
# calculating in-sample loss: LC is c(Female=3.7573, Male=8.8110)
load_model_weights_hdf5(model, file.name)
round(10^4*mean((exp(-as.vector(model %>% predict(x.train)))-exp(-y.train))^2),4)
# calculating out-of-sample loss: LC is c(Female=0.6045, Male=1.8152)
# Female
pred.result <- recursive.prediction.Gender(ObsYear, all_mort2.Female, "Female", T0, tau0, x.min, x.max, model)
vali <- pred.result[[1]][which(all_mort2.Female$Year > ObsYear),]
round(10^4*mean((vali$mx-vali.Y.Female$mx)^2),4)
# Male
pred.result <- recursive.prediction.Gender(ObsYear, all_mort2.Male, "Male", T0, tau0, x.min, x.max, model)
vali <- pred.result[[1]][which(all_mort2.Male$Year > ObsYear),]
round(10^4*mean((vali$mx-vali.Y.Male$mx)^2),4)

6.5.7 稳健性

使用梯度下降法的早期停止解决方案的一个问题是由此产生的校准依赖于算法种子点（起始值）的选择

下图展示使用相同RNN结构、相同超参数和相同校准策略，针对100个不同种子点的选择所画的损失的箱线图

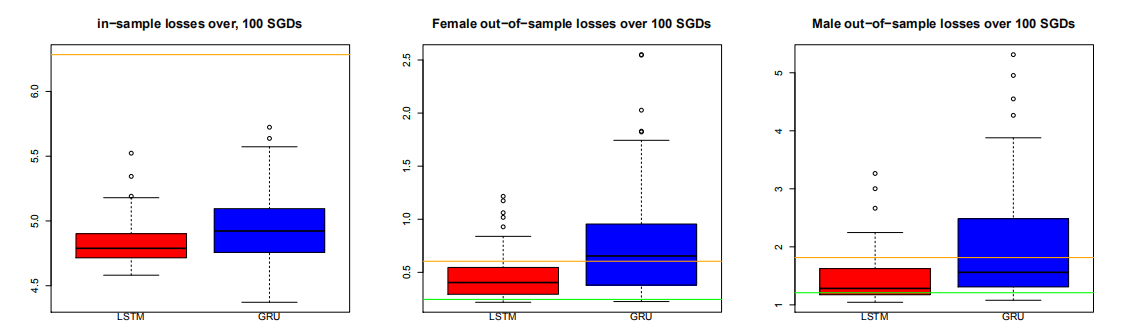
Figure 6.7: 100个不同种子下的损失箱线图

• 红色表示联合性别的LSTM结构中的预测结果；蓝色表示联合性别的GRU结构中的预测；橙色水平线表示的是LC的预测

• 结论：

1. 左侧给出了样本内损失，与LC模型相比，两种RNN结构的样本内损失都有显著减少，平均而言，LSTM的损失比GRU的小，波动性也更小；

2. 中间和右边分别表示女性和男性的样本外损失：不论男性还是女性，LSTM在几乎所有的100次迭代中都比LC模型好；GRU结构尽在大约一半次数的迭代中比LC模型表现好。

• 改进方法：将不同种子点下得到的预测值进行平均，结果如下:

\[ \begin{array}{|l|c|cc|c|} \hline & {\text { in-sample }} & {\text { out-of-sample }} & {\text { out-of-sample }}& {\text { run times }}\\ & \text {both genders} & \text { female } & \text { male } & \text {both genders} \\ \hline \hline \text { LSTM3 }\left(T=10,\left(\tau_{0}, \tau_{1}, \tau_{2}, \tau_{3}\right)=(5,20,15,10)\right) & 4.7643 & 0.3402 & 1.1346 & 404 \mathrm{s}\\ \text { GRU3 }\left(T=10,\left(\tau_{0}, \tau_{1}, \tau_{2}, \tau_{3}\right)=(5,20,15,10)\right) & 4.6311 & 0.4646 & 1.2571 & 379 \mathrm{s} \\ \hline\hline \text { LSTM3 averaged over 100 different seeds} & - & 0.2451 & 1.2093 & 100 \cdot 404\mathrm{s}\\ \text { GRU3 averaged over 100 different seeds } & - & 0.2341& 1.2746 & 100 \cdot 379 \mathrm{s} \\ \hline \hline \text { LC model with SVD } & 6.2841 & 0.6045 &1.8152 & - \\ \hline \end{array} \]

能够看到，平均之后得到了更稳健的解决方案，预测结果也很好，箱线图中绿色水平线表示的就是平均之后的预测损失，显示仅有极少数的在绿色水平线之下的种子点的选择在单独进行校准时效果会更好。

6.5.8 预测结果图

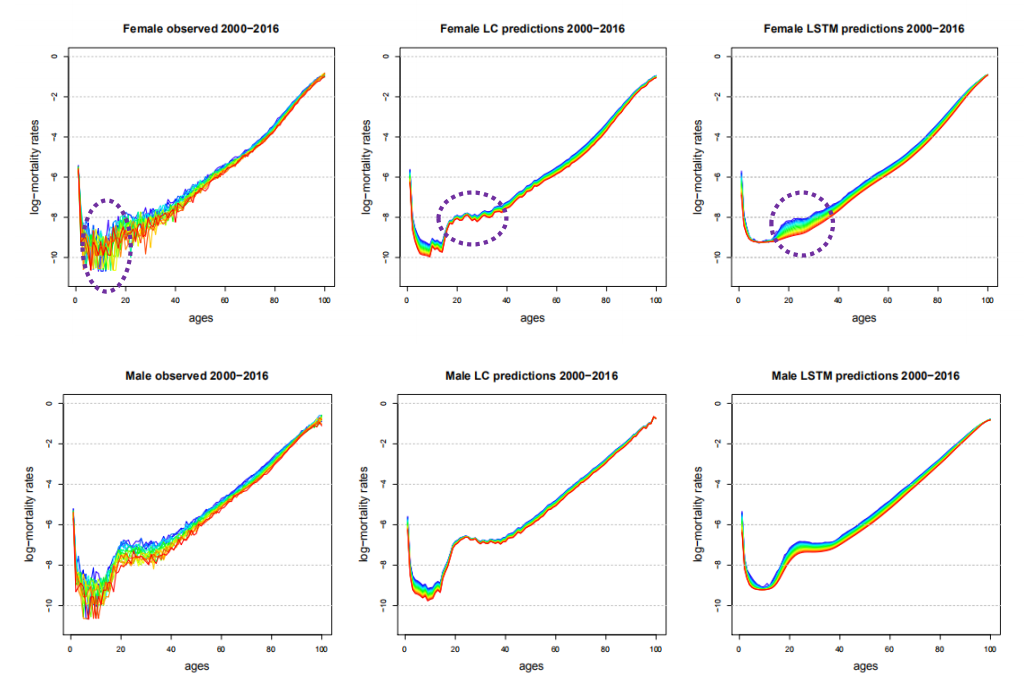
Figure 5.2: 对数死亡率的观察与预测值

结论：

1. 20-40岁之间LSTM方法能够更好的捕捉到死亡率的改善，左边观察值清楚的表明LSTM这样的改善是合理的；

2. 年龄较小人群的死亡率实际改善情况比按照本文方法预测的大，这可能是因为训练数据的青年死亡率改善情况无法代表2000年之后的青年死亡率改善情况。