Chapter 2 Level Annuity

Annuity immediate

\[a_{\overline{n}\mid}=\frac{1-v^n}{i}\] \[s_{\overline{n}\mid}=(1+i)^na_{\overline{n}\mid}=\frac{(1+i)^n-1}{i}\]

Annuity due

\[\ddot{a}_{\overline{n}\mid}=\frac{1-v^n}{d}=(1+i)a_{\overline{n}\mid}=1+a_{\overline{n-1}\mid}\]

\[\ddot{s}_{\overline{n}\mid}=(1+i)^n\ddot{a}_{\overline{n}\mid}\]

Deffered annuity

\[_{m|}a_{\overline{n}\mid}=v^ma_{\overline{n}\mid}=a_{\overline{m+n}\mid}-a_{\overline{n}\mid}\]

Perpetuity

\[a_{\overline{\infty}\mid}=\frac{1}{i}\] \[\ddot{a}_{\overline{\infty}\mid}=\frac{1}{d}\]

\(m\)-thly payable annuity

\[a^{(m)}_{\overline{n}\mid}=\frac{1-v^n}{i^{(m)}}=\frac{i}{i^{(m)}}a_{\overline{n}\mid}\] \[\ddot{a}^{(m)}_{\overline{n}\mid}=\frac{1-v^n}{d^{(m)}}=\frac{d}{d^{(m)}}{\ddot{a}}_{\overline{n}\mid}\] \[a^{(m)}_{\overline{\infty}\mid}=\frac{1}{i^{(m)}}\] \[\ddot{a}^{(m)}_{\overline{\infty}\mid}=\frac{1}{d^{(m)}}\] \[\ddot{a}^{(m)}_{\overline{\infty}\mid}=(1+i)^{1/m}a^{(m)}_{\overline{\infty}\mid}\]

Continuous payable annuity

\[\bar{a}_{\overline{n}\mid}=\frac{i}{\delta}{a}_{\overline{n}\mid}=\frac{d}{\delta}\ddot{a}_{\overline{n}\mid}=\frac{1-v^n}{\delta}\] \[\bar{a}_{\overline{\infty}\mid}=\frac{1}{\delta}\]

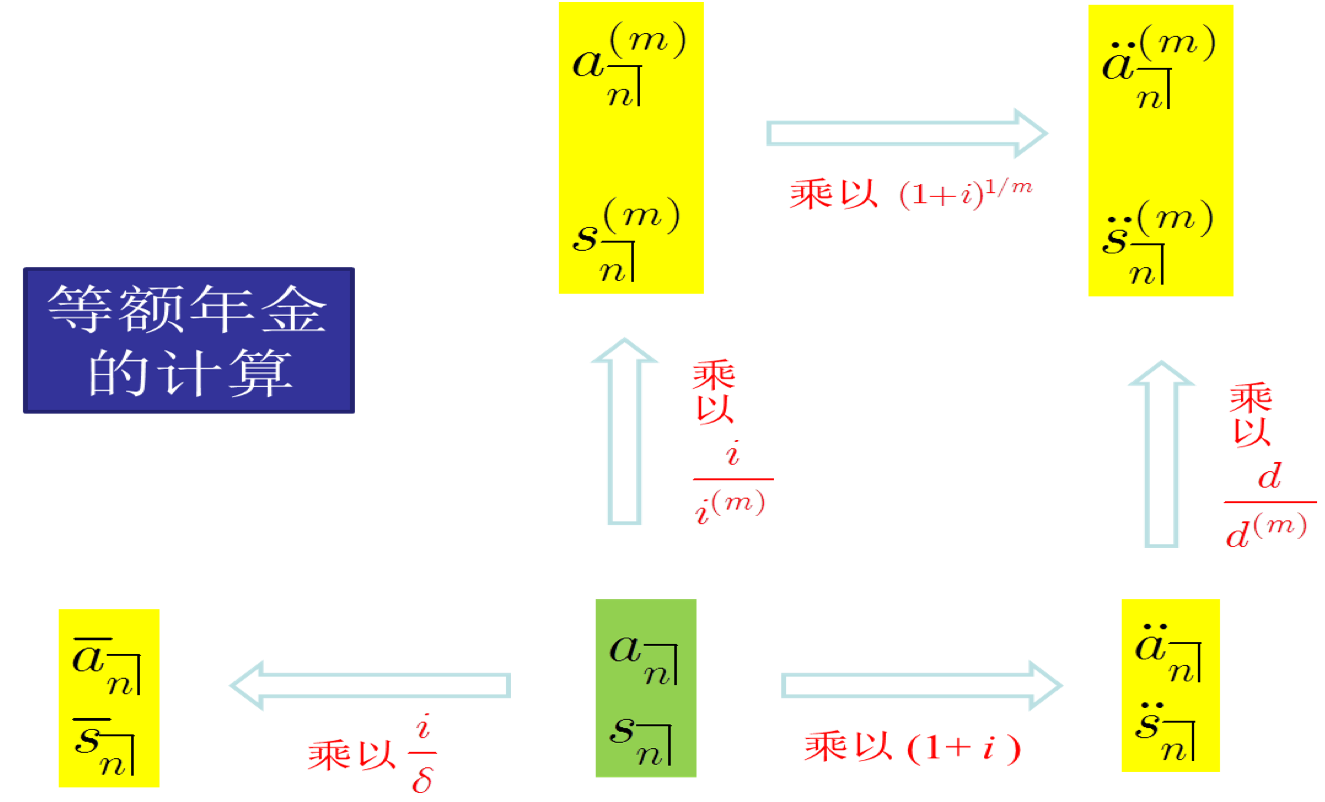
Key relations